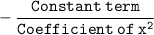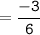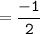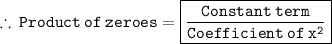★ The polynomial
f(x) = 6x² - 3
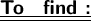
★ Zeroes of the polynomial f(x) = 6x² - 3

We have,
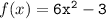
Which can also be written as
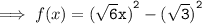
Using a² - b² = (a - b) (a + b)
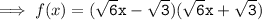
To find the zeroes, solve f(x) = 0
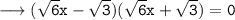
either
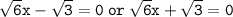
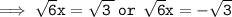
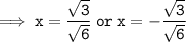
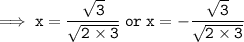
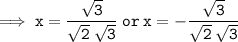
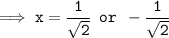
Hence, the zeroes of f(x) = 6x² - 3 are:
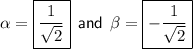
• Verification
Sum of zeroes =
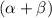
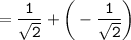
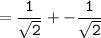
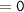
and,
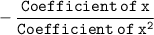
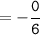
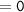
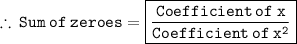
Also,
Product of zeroes =
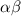
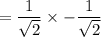
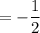
and,