Question

Which statement describes the vertical asymptotes of the graph of f(x)=x^2-64/8x-64

O The graph has no vertical asymptote.
O The graph has a vertical asymptote at x = 8 only.
O The graph has a vertical asymptote at x = -8 only.
O The graph has vertical asymptotes at both x = 8 and x = -8.

Answer 1

Answer: Choice A

The graph has no vertical asymptote

===========================================================

Step-by-step explanation:

Let's simplify the function by factoring each piece.

`f(x) = (x^2-64)/(8x-64)\\\\f(x) = ((x-8)(x+8))/(8x-64)\\\\f(x) = ((x-8)(x+8))/(8(x-8))\\\\f(x) = (x+8)/(8)\\\\`

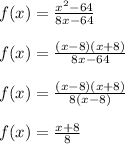
In the 2nd step, I used the difference of squares rule to factor the numerator. In the 4th step, the (x-8) terms cancel.

The simplified version doesn't have any variables in the denominator. This indicates the denominator is always 8, and never 0. So it's impossible to divide by zero in this simplified form. Consequently it means this graph has no vertical asymptotes.

However, there is a hole at x = 8 because this input causes a division by zero error in the original non-simplified function. Why? Because the calculator will use PEMDAS to evaluate the expression after replacing every copy of x with 8. It likely won't attempt to simplify like shown in the steps above. This is what causes the hole at x = 8.

The value x = -8 is perfectly fine in either the original function or the simplified one. It doesn't cause the denominator to be zero.