Question

F. How many times greater is the area of triangle DEF

than the area of triangle ABC? Show/explain.

Answer 1

Area of ΔDEF is 2.25 times the area of ΔABC.

Explanation:

Since, ΔDEF is the enlarged form of ΔABC,

Scale factor =
`\frac{\text{Side length of triangle ABC}}{\text{Corresponding side length of image triangle}}`

=
`(15)/(10)`

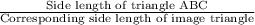
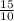
= 1.5

Since, ratio of the areas of image and preimage triangles = (Scale factor)²

`\frac{\text{Area of image triangle}}{\text{Area of triangle ABC}}` = (Scale factor)²

`\frac{\text{Area of image triangle}}{\text{Area of triangle ABC}}=(1.5)^2`

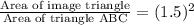
Area of image ΔDEF = 2.25(Area of ΔABC)

Therefore, area of ΔDEF is 2.25 times the area of ΔABC.