Answer:
By putting both values of x in the expression, it can be concluded that both expressions are equivalent.
Explanation:
The expressions can be evaluated to be equivalent by putting the values given
The expressions are:
8x+40 and 8(x+5)
Putting x = 6 in both
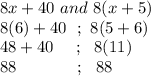
The values of both expressions are same on x=6
Now putting x = 10

The values of both expressions are same on x = 10
Hence,
By putting both values of x in the expression, it can be concluded that both expressions are equivalent.