Question

5) Diseñar un sistema de ecuaciones lineales y resolverlo a través del método de Gaussiana, que permita resolver el siguiente problema: -Un ingeniero realiza las siguientes observaciones sobre las ventas de impresoras en una tienda: Hay impresoras Epson, Hp y Cannon. El número de impresoras Epson y Hp es cinco veces el número de las Cannon. Además, el número de impresoras Epson es el triple que el de la Cannon y el total de impresoras Cannon y Hp asciende a 12.

Answer 1

`X=12`

`Y=8`

`Z=4`

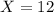
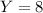
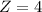
Explanation:

Comencemos definiendo las variables ⇒

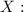`X:` '' Número de impresoras Epson ''

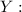`Y:` '' Número de impresoras Hp ''

`Z:` '' Número de impresoras Cannon ''

Ahora , dado que tenemos las variables definidas podemos escribir el sistema de ecuaciones lineales

''El número de impresoras Epson y Hp es cinco veces el número de las Cannon''

Para esa oración escribimos la siguiente ecuación :

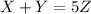`X+Y=5Z` (I) que se puede reescribir como

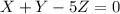`X+Y-5Z=0` (II)

''El número de impresoras Epson es el triple que el de las Cannon''

Para esa oración escribimos la siguiente ecuación :

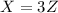`X=3Z` (III) que se puede reescribir como

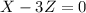`X-3Z=0` (IV)

''El total de impresoras Cannon y Hp asciende a 12''

Para ésta última frase escribimos la última ecuación :

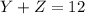`Y+Z=12` (V)

Con (II), (IV) y (V) armamos el sistema de ecuaciones lineales :

`X+Y-5Z=0\\X-3Z=0\\Y+Z=12`

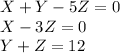
Lo resolvemos a través del método de Gauss insertando el sistema en una matriz y realizando operaciones de fila entre las respectivas filas de la matriz :

`\left[\begin{array}{ccxc}1&1&-5&0\\1&0&-3&0\\0&1&1&12\end{array}\right]`

Realizando operaciones entre filas se lleva a la siguiente matriz equivalente :

`\left[\begin{array}{cccc}1&1&-5&0\\0&-1&2&0\\0&0&3&12\end{array}\right]` En esta matriz el sistema de ecuaciones asociado es

`X+Y-5Z=0\\-Y+2Z=0\\3Z=12`

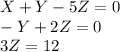
De aquí encontramos que
`Z=4` ,
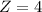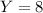`Y=8` y
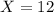`X=12` (encontramos primero el valor de
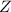`Z` en la última ecuación, de allí reemplazamos en la segunda ecuación para hallar el valor de
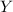`Y`. Finalmente el valor de
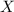`X` se calcula con la primera ecuación)

La solución a éste sistema de ecuaciones es

`X=12`

`Y=8`

`Z=4`

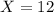
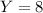
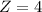
Es recomendable reemplazar éstos valores en el sistema original para verificarlos.