Question

HELPPPPPPPPPPPPPPPPPPPPPPPPPP

Answer 1

If you are in calculus, then you would apply the derivative to get

h(x) = x^2 - 2x + 3

h ' (x) = 2x - 2

The gradient, or slope of the tangent line, is negative when the derivative is negative.

So we need to solve h ' (x) < 0.

h ' (x) < 0

2x-2 < 0

2x < 2

x < 2/2

x < 1

Any x value smaller than x = 1 will lead to a negative gradient.

-----------------------------------

If you are not in calculus, then you can determine the vertex of the function

Note that y = x^2 - 2x + 3 is in the form y = ax^2 + bx + c with

a = 1

b = -2

c = 3

The x coordinate of the vertex is

h = -b/(2a)

h = -(-2)/(2*1)

h = 1

The x coordinate of the vertex is x = 1. Anything to the left of this will represent a negative gradient. This is because the given parabola opens upward (note how a = 1 is positive).

The graph goes downhill on the interval
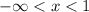`-\infty < x < 1` and it goes uphill on the interval
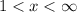`1 < x < \infty` as shown below.