Answer:
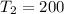
Explanation:
Given
Geometry Progression
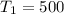

Required
Calculate the second term
First, we need to write out the formula to calculate the nth term of a GP
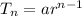
For first term: Tn = 500 and n = 1
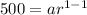
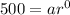
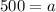
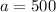
For fought term: Tn = 32 and n = 4
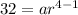
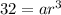
Substitute 500 for a
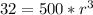
Make r^3 the subject
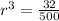
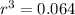
Take cube roots
![\sqrt[3]{r^3} = \sqrt[3]{0.064}](https://img.qammunity.org/2021/formulas/mathematics/college/6kn8cjh9xh9nhgjqxbk2t7e68tgsefqkra.png)
![r = \sqrt[3]{0.064}](https://img.qammunity.org/2021/formulas/mathematics/college/22pif4ah022r8uwvfxrv13hul6kjgh3zrh.png)

Using:
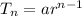

 and
and
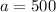
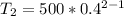

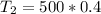
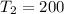
Hence, the second term is 200