Answer:
The system of inequalities is -2x + y > 0 -x + y ≥ 0
Explanation:
The form of the equation of a line is y = m x + b, where
The line passes through the origin, then
- The form of the equation is y = m x
Let us look at the graph to find the correct answer
∵ One of the lines are solid and the other is dashed
∵ The shaded area is over the two lines
∴ The signs of the two inequalities are ≥ and >
∵ The two lines pass through the origin
→ That means the y-intercepts are 0
∴ The form of the inequalities are y ≥ m
 x and y > m
x and y > m

There are only two answers that have these forms, so we must find the slope of each line
∵ m =
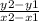 , (x1, y1) and (x2, y2) are two points on the line
, (x1, y1) and (x2, y2) are two points on the line
∵ The solid line passes through points (0, 0) and (2, 2)
∴ m
 =
=
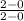 =
=
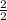 = 1
= 1
→ Substitute it in the form of the equation
∴ y ≥ 1(x)
∴ y ≥ x
→ Subtract x from both sides
∴ -x + y ≥ 0
∵ The dashed line passes through points (0, 0) and (1, 2)
∴ m
 =
=
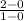 =
=
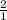 = 2
= 2
→ Substitute it in the form of the equation
∴ y > 2(x)
∴ y > 2x
→ Subtract 2x from both sides
∴ -2x + y > 0
The system of inequalities is -2x + y > 0 -x + y ≥ 0