Answer:
The maximum water pressure at the discharge of the pump (exit) = 496 kPa
Step-by-step explanation:
The equation expressing the relationship of the power input of a pump can be computed as:
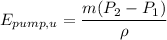
where;
m = mass flow rate = 120 kg/min
the pressure at the inlet
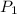 = 96 kPa
= 96 kPa
the pressure at the exit
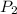 = ???
= ???
the pressure
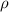 = 1000 kg/m³
= 1000 kg/m³
∴
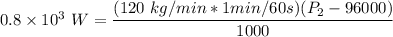
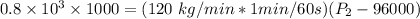
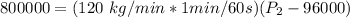
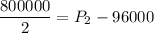
400000 = P₂ - 96000
400000 + 96000 = P₂
P₂ = 496000 Pa
P₂ = 496 kPa
Thus, the maximum water pressure at the discharge of the pump (exit) = 496 kPa