Answer:
A
Explanation:
We have:

And we want to isolate x₂.
So, let’s first remove the denominator by multiplying both sides by it:
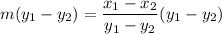
The right side will cancel. This will leave:
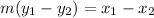
Now, we can subtract x₁ from both sides. So:
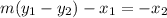
Finally, we will multiply both sides by -1. So:
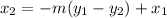
Hence, our answer is A.