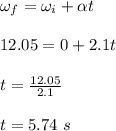Question

A wheel turns through 5.5 revolutions while being accelerated from rest at 20rpm/s.(a) What is the final angular speed ? (b) How long does it take to turn the 5.5 revolutions?

Answer 1

(a) The final angular speed is 12.05 rad/s

(b) The time taken to turn 5.5 revolutions is 5.74 s

Step-by-step explanation:

Given;

number of revolutions, θ = 5.5 revolutions

acceleration of the wheel, α = 20 rpm/s

number of revolutions in radian is given as;

θ = 5.5 x 2π = 34.562 rad

angular acceleration in rad/s² is given as;

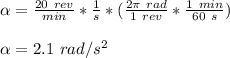
`\alpha = (20 \ rev)/(min) *(1)/(s) *((2\pi \ rad)/(1 \ rev ) *(1 \ min)/(60 \ s)) \\\\\alpha = 2.1 \ rad/s^2`

(a)

The final angular speed is given as;

`\omega _f^2 = \omega_i ^2 + 2\alpha \theta\\\\\omega _f^2 = 0 + 2\alpha \theta\\\\\omega _f^2 = 2\alpha \theta\\\\\omega _f = √(2\alpha \theta)\\\\ \omega _f = √(2(2.1) (34.562))\\\\ \omega _f = 12.05 \ rad/s`

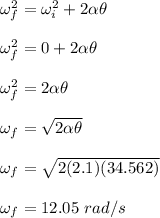
(b) the time taken to turn 5.5 revolutions is given as

`\omega _f = \omega _i + \alpha t\\\\12.05 = 0 + 2.1t\\\\t = (12.05)/(2.1) \\\\t = 5.74 \ s`