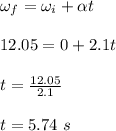Answer:
(a) The final angular speed is 12.05 rad/s
(b) The time taken to turn 5.5 revolutions is 5.74 s
Step-by-step explanation:
Given;
number of revolutions, θ = 5.5 revolutions
acceleration of the wheel, α = 20 rpm/s
number of revolutions in radian is given as;
θ = 5.5 x 2π = 34.562 rad
angular acceleration in rad/s² is given as;
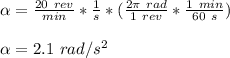
(a)
The final angular speed is given as;
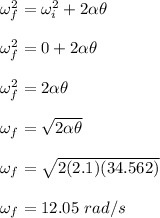
(b) the time taken to turn 5.5 revolutions is given as