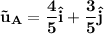Question

Find the unit vector in the direction of vector A=4i +3j

Answer 1

`\displaystyle \vec u_A=(4)/(5)\hat i +(3)/(5)\hat j`

Step-by-step explanation:

Unit Vector

The unit vector associated with a given vector
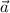`\vec a` is another vector pointing in the same direction of
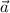`\vec a` and with magnitude 1.

The unit vector can be calculated as follows:

`\displaystyle \vec u_a=(\vec a )/(||\vec a ||)`

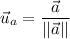
Where
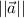`||\vec a ||` is the magnitude of the vector.

If
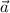`\vec a` is given as:

`\vec a = x\hat i +y\hat j`

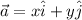
The magnitude of the vector is:

`=√(x^2+y^2)`

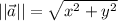
We have:

`\vec A=4\hat i +3\hat j`

`=√(4^2+3^2)=√(25)=5`

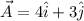
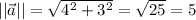
Thus the unit vector is:

`\displaystyle \vec u_A=(4\hat i +3\hat j )/(5)`

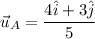
Simplifying:

`\mathbf{\displaystyle \vec u_A=(4)/(5)\hat i +(3)/(5)\hat j}`