Answer:
No solutions.
General Formulas and Concepts:
Pre-Algebra
- Order of Operations: BPEMDAS
- Equality Properties
Algebra I
- Solving systems of equations using substitution/elimination
- Solving systems of equations by graphing
- Expanding
- Finding roots of a quadratic
- Standard Form: ax² + bx + c = 0
- Quadratic Formula:
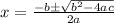
Explanation:
Step 1: Define systems
2x - y = 9
4x² + 3y² - 2x + y = 16
Step 2: Rewrite systems
2x - y = 9
- Subtract 2x on both sides: -y = 9 - 2x
- Divide -1 on both sides: y = 2x - 9
Step 3: Redefine systems
y = 2x - 9
4x² + 3y² - 2x + y = 16
Step 4: Solve for x
Substitution
- Substitute in y: 4x² + 3(2x - 9)² - 2x + (2x - 9) = 16
- Expand: 4x² + 3(4x² - 36x + 81) - 2x + (2x - 9) = 16
- Distribute 3: 4x² + 12x² - 108x + 243 - 2x + 2x - 9 = 16
- Combine like terms: 16x² - 108x + 234 = 16
- Factor GCF: 2(8x² - 54x + 117) = 16
- Divide 2 on both sides: 8x² - 54x + 117 = 8
- Subtract 8 on both sides: 8x² - 54x + 109 = 0
- Define variables: a = 8, b = -54, c = 109
- Resubstitute:

- Exponents:
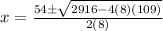
- Multiply:
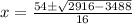
- Subtract:
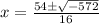
Here we see that we start to delve into imaginary roots. Since on a real number plane, we do not have imaginary roots, there would be no solution to the systems of equations.
Step 5: Graph systems
We can verify our results.