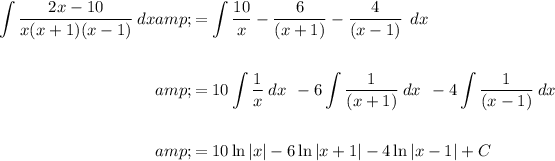Answer:
First, express the fraction in partial fractions
Write it out as an identity:
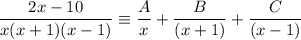
Add the partial fractions:
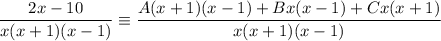
Cancel the denominators from both sides of the original identity, so the numerators are equal:

Now solve for A, B and C by substitution.
Substitute values of x which make one of the expressions equal zero (to eliminate all but one of A, B and C):
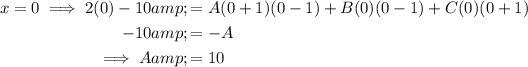

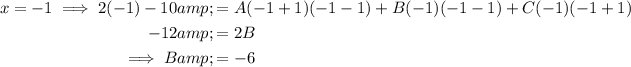
Replace the found values of A, B and C in the original identity:
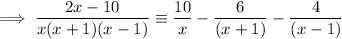
Now integrate: