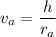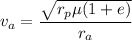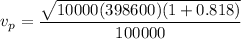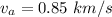Question

An unmanned satellite orbits the earth with a perigee radius of 10,000 km and an apogee radius of 100,000 km. Calculate:

a. the eccentricity of the orbit
b. the semimajor axis of the orbit(km)
c. the period of the orbit(hours)
d. the specific energy of the orbit(km^2/s^2)
e. the true anomaly at which the altitude is 1000km (degrees)
f. Vr and V(perpendicular) at the points found in part (e) (km/s)
g. the speed at the perigee and apogee (km/s)

Answer 1

Given :

radius of perigee,
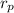`$r_p$` = 10,000 km

radius of apogee,
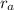`$r_a$` = 100,000 km

a). Eccentricity of the orbit

`$e=(|r_p-r_a|)/(r_p+r_a)$`

`$e=(|10,000-100,000|)/(10,000+100,000)$`

`$e=(9)/(11)$`

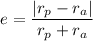
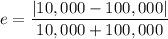
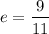
or e = 0.818

b). Semi major axis of the orbit

`$a=(r_p+r_a)/(2)$`

`$a=(10,000+100,000)/(2)$`

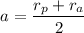
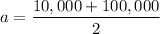
= 55,000 km

c). period of orbit

`$T=(2\pi)/(√(\mu))* a^(3/2)$`

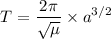
Replacing μ with
`$398600 \ km^3/s^2$`

`$T=(2\pi)/(√(398600))* (55,000)^(3/2)$`

`$T=128304.04 \ s \left((1 \ hr)/(3600 \ s)\right)$`

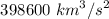
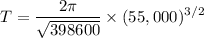
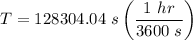
T = 35.64 hr

d). Specific energy of the orbit

`$\varepsilon = -(\mu)/(2a)$`

`$\varepsilon = -(398600)/(2 * 55000)$`

`$\varepsilon = -3.62 \ km^2/s^2$`

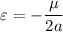
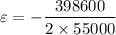
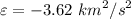
e). the equation of the distance to the focus

`$\theta = \cos^(-1)\left((a(1-e^2))/(r)-(1)/(e)\right)$`

`$\theta = \cos^(-1)\left((55000(1-(0.818)^2))/((1000+6378))-(11)/(9)\right)$`

`$\theta = \cos^(-1)\left((55000(0.33))/((7378))-(11)/(9)\right)$`

`$\theta = \cos^(-1)\left(2.4-1.2\right)$`

`$\theta = \cos^(-1)\left(1.2\right)$`

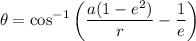
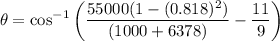
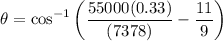
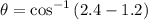
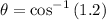
θ = 1.002°

f).Calculating the angular momentum

`$r_p=(h^2)/(\mu(1+e))$`

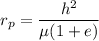
or
`$h=√(r_p \mu(1+e))$`

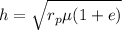
Now calculate the radial velocity

`$v_r=(\mu)/(h) e \sin \theta$`

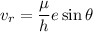
Substituting for h,

`$v_r=(\mu)/(h)e \sin \theta$`

`$v_r=(e\mu \sin \theta)/(√(r_p \mu(1+e)))$`

`$v_r=((9)/(11)√(398600) \sin 20)/(√(10,000 (1+0.818)))$`

`$v_r= 1.30 \ km/s$`

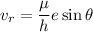
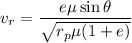
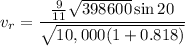
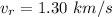
Now calculating the azimuthal velocity

`$v_(\perp)=(\mu)/(h)(1+e \cos \theta)$`

`$v_(\perp)=(\mu (1+e \cos \theta))/(√(r_p \mu(1+e)))$`

`$v_(\perp)=(√(398600) (1+0.818 \cos 20))/(√(10000(1+0.818)))$`

`$v_(\perp)=7.58 \ km/s$`

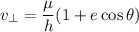
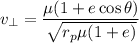
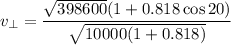
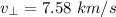
g). Velocity at perigee

`$v_p=(h)/(r_p)$`

`$v_p=(√(r_p \mu (1+e)))/(r_p)$`

`$v_p=(√(10000 (398600) (1+0.818)))/(10000)$`

`$v_p=8.52 \ km/s$`

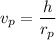
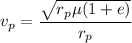
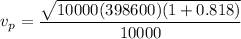
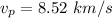
Now calculate the velocity of the apogee

`$v_a=(h)/(r_a)$`

`$v_a=(√(r_p \mu (1+e)))/(r_a)$`

`$v_p=(√(10000 (398600) (1+0.818)))/(100000)$`

`$v_a= 0.85 \ km/s$`