Answer:
The probability that a randomly chosen widget weighs more then 19 grams is 0.468.
Explanation:
X = Widget weights produced at Acme Widget Works
It is provided that X is normally distributed with mean 17.46 grams and variance 375.67 grams.
Compute the probability that a randomly chosen widget weighs more then 19 grams as follows:
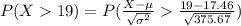
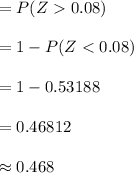
Thus, the probability that a randomly chosen widget weighs more then 19 grams is 0.468.