Question

Suppose widgit weights produced at Acme Widgit Works have weights that are normally distributed with mean 17.46 grams and variance 375.67 grams. What is the probability that a randomly chosen widgit weighs more then 19 grams?

Answer 1

The probability that a randomly chosen widget weighs more then 19 grams is 0.468.

Explanation:

X = Widget weights produced at Acme Widget Works

It is provided that X is normally distributed with mean 17.46 grams and variance 375.67 grams.

Compute the probability that a randomly chosen widget weighs more then 19 grams as follows:

`P(X>19)=P(\frac{X-\mu}{\sqrt{\sigma^(2)}}>(19-17.46)/(√(375.67)))`

`=P(Z>0.08)\\\\=1-P(Z<0.08)\\\\=1-0.53188\\\\=0.46812\\\\\approx 0.468`

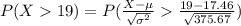
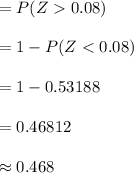
Thus, the probability that a randomly chosen widget weighs more then 19 grams is 0.468.