Question

The length of a rectangle is 5 inches more than its vedth. The area of the rectangle is equal to

2 inches more than 4 times the perimeter. Find the length and width of the rectangle.

Answer 1

• The width = x = 14

• The length = x+5 = 14+5 = 19

Explanation:

Let l = length, w = width, A = area = l×w , and P = perimeter = 2(l+w)

Let 'x' be the width

As the length 'l' of a rectangle is 5 inches more than its width.

so the length will be = x+5

As the Area of the rectangle is equal to 2 inches more than 4 times the perimeter.

A = 4P + 2

so the equation becomes

l × w = 4×2(l+w)+2

substituting w=x, l = x+5,

(x+5)x = 8(x+5+x)+2

x²+5x = 8(5+2x)+2

x²+5x = 40+16x+2

x²+5x = 16x+42

x²+5x-16x-42 =0

x²-11x-42=0

`x^2-11x=42`

`\mathrm{Add\:}a^2=\left(-(11)/(2)\right)^2\mathrm{\:to\:both\:sides}`

`x^2-11x+\left(-(11)/(2)\right)^2=42+\left(-(11)/(2)\right)^2`

`x^2-11x+\left(-(11)/(2)\right)^2=(289)/(4)`

`\left(x-(11)/(2)\right)^2=(289)/(4)`

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

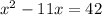
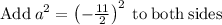
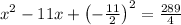
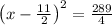
solving

`x-(11)/(2)=\sqrt{(289)/(4)}`

`x-(11)/(2)=(√(289))/(√(4))`

`x-(11)/(2)=(√(289))/(2)`

`x-(11)/(2)=(17)/(2)`

`x-(11)/(2)+(11)/(2)=(17)/(2)+(11)/(2)`

`x=14`

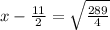
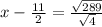
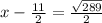
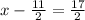
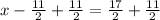
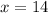
similarly solving

`x-(11)/(2)=-\sqrt{(289)/(4)}`

`x-(11)/(2)=-(17)/(2)`

`x-(11)/(2)+(11)/(2)=-(17)/(2)+(11)/(2)`

`x=-3`

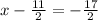
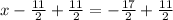
so

x = 14, or x = -3

As the width 'x' can not be negative.

so x = 14

Thus,

• The width = x = 14

• The length = x+5 = 14+5 = 19