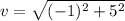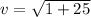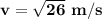Question

The x and y coordinates of a particle at any time t are x = 5t - 3t2 and y = 5t respectively, where x and y are in meter and t in second. The speed of the particle at t = 1 second is​

Answer 1

`v=√(26)~m/s`

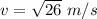
Step-by-step explanation:

Parametric Equation of the Velocity

Given the position of the particle at any time t as

`r(t) = (x(t),y(t))`

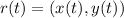
The instantaneous velocity is the first derivative of the position:

`v(t)=(v_x(t),v_y(t))=(x'(t),y'(t))`

The speed can be calculated as the magnitude of the velocity:

`v=√(v_x^2+v_y^2)`

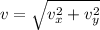
We are given the coordinates of the position of a particle as:

`x=5t-3t^2`

`y=5t`

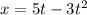
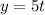
The coordinates of the velocity are:

`v_x(t)=(5t-3t^2)'=5-6t`

`v_y(t)=(5t)'=5`

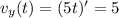
Evaluating at t=1 s:

`v_x(1)=5-6(1)=-1`

`v_y(1)=5`

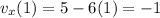
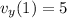
The velocity is:

`v=√((-1)^2+5^2)`

`v=√(1+25)`

`\mathbf{v=√(26)~m/s}`