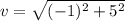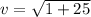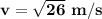Answer:
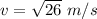
Step-by-step explanation:
Parametric Equation of the Velocity
Given the position of the particle at any time t as
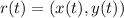
The instantaneous velocity is the first derivative of the position:
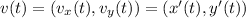
The speed can be calculated as the magnitude of the velocity:
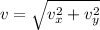
We are given the coordinates of the position of a particle as:
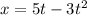
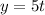
The coordinates of the velocity are:
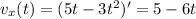
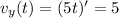
Evaluating at t=1 s:
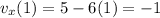
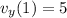
The velocity is: