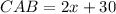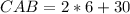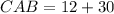Question

AB is the bisector of CAD. If the mCAB = 2x+30 and m DAB=5x+12 what is the mCAB

Answer 1

`CAB = 42`

Explanation:

Given

`CAB = 2x + 30`

`DAB = 5x + 12`

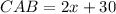
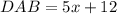
Bisector: AB

Required

Find CAB

Since AB bisects CAD, then

`CAB = DAB`

This is so because AB divides CAD into two equal parts which are CAB and DAB

`CAB = DAB`

Substitute values for CAB and DAB

`2x + 30 = 5x + 12`

Collect Like Terms

`2x- 5x = 12 - 30`

`-3x = -18`

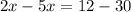
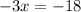
Divide both sides by -3

`x = 6`

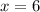
To solve for CAB, we simply substitute 6 for x in
`CAB = 2x + 30`

`CAB = 2 * 6 + 30`

`CAB = 12 + 30`

`CAB = 42`