Answer:
The function is odd
Explanation:
Even functions and odd functions are those which satisfy particular symmetry relations as follows:
f(x) is even if f(-x) = f(x)
f(x) is odd if f(-x) = -f(x)
Not all functions are eligible for being even or odd.
Considering
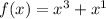
Let's find f(-x)
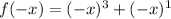
Since
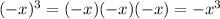
And
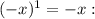
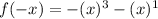
Factoring by -1:
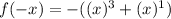
The expression in parentheses if f(x), thus:

And the function is odd.