Answer:
Pythagorean identity sin²θ+cos²θ = 1 is true for the angle θ =

Explanation:
At first, let us simplify the left side of the identity
∵ The left side is sin²Ф + cos²Ф
∵ Ф =
 ⇒ lies in the 4th quadrant
⇒ lies in the 4th quadrant
∴ The left side is sin²(
 ) + cos²(
) + cos²(
 )
)
→ Let us write the values of sin(
 ) and cos(
) and cos(
 )
)
∵ sin(
 ) =
) =
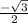 ⇒ sine an angle in the 4th quadrant is -ve
⇒ sine an angle in the 4th quadrant is -ve
∵ cos(
 ) =
) =
 ⇒ cosine an angle in the 4th quadrant is +ve
⇒ cosine an angle in the 4th quadrant is +ve
→ Substitute them in the left side
∵ sin²(
 ) + cos²(
) + cos²(
 ) = [
) = [
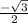 ]² + [
]² + [
 ]²
]²
∴ sin²(
 ) + cos²(
) + cos²(
 ) = [
) = [
 ] + [
] + [
 ]
]
∴ sin²(
 ) + cos²(
) + cos²(
 ) = [
) = [
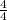 ]
]
∴ sin²(
 ) + cos²(
) + cos²(
 ) = 1
) = 1
∵ The right side = 1
∴ Left side = Right side
∴ sin²(
 ) + cos²(
) + cos²(
 ) = 1 ⇒ proved
) = 1 ⇒ proved
∴ Pythagorean identity sin²θ+cos²θ = 1 is true for the angle θ =
