Answer:
The dimensions of the largest shed are 17 ft by 17 ft.
The area of the largest shed is 289 sq ft.
Explanation:
Given that:
Fixed perimeter of the rectangular shed = 68 ft
To find:
The dimensions of the largest shed that can be built = ?
And
Area of the largest shed that can be built = ?
Solution:
First of all, let us have a look at the formula for perimeter of a rectangular shape shed:
Perimeter of a rectangle = 2
 (Length + Width)
(Length + Width)
68 = 2
 (Length + Width)
(Length + Width)
Length + Width = 34
The largest possible values are only in the case when the rectangle is a square.
i.e. Length = Width
Therefore values of length and width are:
Length = Width =

Area of a square is given by the formula:
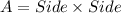
 = 17
= 17
 17 = 289 sq ft
17 = 289 sq ft
The answer is:
The dimensions of the largest shed are 17 ft by 17 ft.
The area of the largest shed is 289 sq ft.