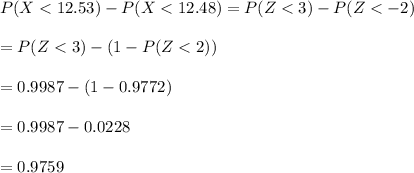Question

Let's assume your process yields products with a mean diameter of 12.50mm and σ = 0.010mm. If the specification calls for a range of 12.480mm - 12.530mm, what percentage of parts will have a diameter within these limits?

Answer 1

There is a 97.59% that diameter of the product will fall in the specified range.

Explanation:

Let X be the r.v. the diameter of a product

X~N(12.5, (0.010)²)

P(12.48 < X < 12.53) = P(X < 12.53) - P(X < 12.48)

Convert the x-values to corresponding z-values

`Z_(1) = (12.48 - 12.50)/(0.01) = -2\\\\Z_(2) = (12.53 - 12.50)/(0.01) = 3\\\\`

Then, using the standard normal distribution cumulative probability tables:

`P(X < 12.53) - P(X < 12.48) = P(Z < 3) - P(Z < -2)\\\\= P(Z < 3) - (1 - P(Z < 2))\\\\= 0.9987 - (1 - 0.9772)\\\\= 0.9987 - 0.0228\\\\= 0.9759`