Answer:
See Explanation
Explanation:
3.
XY is tangent at P and CP is radius
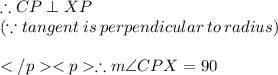
4.
Radius of the circle = diameter /2 = 13/2 = 6.5.cm
5.
For BD to be be tangent to the circle with center C, BD should make right angle with radius CB.
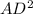 should be equal to the sum of the squares BD and AB.
should be equal to the sum of the squares BD and AB.
Let us work it out:
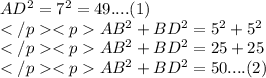
From equations (1) & (2), it is obvious that:
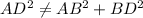
So, BD is not tangent to the
6.
Tangents drawn from an external point to a circle are congruent.
In circle with center C, BA and BD are tangents drawn from external point B.
Therefore,
BA = BD
x = 4
7.
In circle with center C, BA and BD are tangents drawn from external point B.
Therefore,
BD = BA (tangents drawn from external point to a circle)
x = 2
8.
In circle with center C, BA and BD are tangents drawn from external point B.
Therefore,
BA = BD (tangents drawn from external point to a circle)
2x = 10
x = 10/2
x = 5