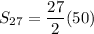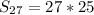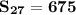Question

I need help with this question.

Answer 1

`\displaystyle S_(27)=675`

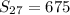
Explanation:

The sum of N consecutive natural numbers is given by:

`\displaystyle S_N=(N)/(2)(F+L)`

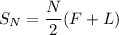
We need to find the sum of the natural numbers between 12 to 38.

To calculate the required sum we have F=12, L=38, but we don't have the value of N.

From 12 to 38 there are 38 - 12 + 1 = 27 natural consecutive numbers, thus N=27.

Substituting in the formula:

`\displaystyle S_(27)=(27)/(2)(12+38)`

`\displaystyle S_(27)=(27)/(2)(50)`

`\displaystyle S_(27)=27*25`

`\mathbf{\displaystyle S_(27)=675}`