Answer:
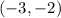
Explanation:
First, you need to get one like term in each equation the same in order to eliminate. To do less damage to the equation, we'll use the x terms.
To get the x terms the same, multiply both equations by the opposite x term:
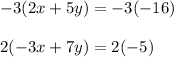
Simplify by multiplying. Use the distributive property for the left side (remember, two negatives make a positive and a negative multiplied by a positive will always be negative):
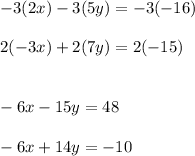
Now subtract all like terms. The x terms cancel out:

Now solve the new equation for y. Isolate the variable by using inverse operations. The term can be seen as -29×y. In order to isolate the variable, use division (opposite of multiplication). Divide both sides by 29:

Make the variable positive. Multiply both sides by -1:
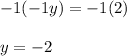
The value of y is -2. Insert this value into either original equation:

Solve for x. Simplify multiplication:
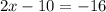
Use inverse operations to get like terms on the same side of the equation. Add 10 to both sides (addition is the opposite of subtraction) to cancel out the -10 on the left:

Isolate the variable using inverse operations. The x term can be seen as 2×x. Division is the opposite of multiplication, so divide both sides by 2:
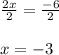
The value of x is -3. Therefore, the solution to the system is:
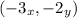
:Done