Question

La expresión que se muestra abajo re presenta la utilidad en la producción de una nueva libreta profesional ,¿para que el valor positivo "X" la utilidad resulta igual a cero?

a)10
b)10/9
c)770/9
d)670/9
ayúdenme porfavor​

Answer 1

Answer: a) 10

Explanation:

Buscando en google, encuentro que la expresión es:

C(x) = 9*x^2 - 80*x - 100

Queremos encontrar el valor de x (positivo), tal que esa expresión sea igual a cero, entonces tenemos que resolver:

9*x^2 - 80*x - 100 = 0.

Para ello podemos recordar la ecuación de Bhaskara, que para una ecuación de la forma:

a*x^2 + b*x + c = 0

Las soluciones son:

`x = (-b +-√(b^2 - 4*a*c) )/(2a)`

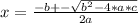
en este caso, tenemos:

a = 9

b = -80

c = -100

Entoces, las soluciones van a ser:

`x = (-(-80) +- √((-80)^2 - 4*9*(-100)) )/(2*9) = (80 +- 100)/(18)`

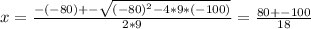
Entonces las dos soluciones son:

x = (80 - 100)/18 = -20/18 = -10/9

Esta solución la descartamos, pues es negativa. La otra solución es:

x = (80 + 100)/18 = 180/18 = 10

La opción correcta es a: 10