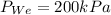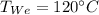Question

A well-insulated heat exchanger has one line with 2 kg/s of air at 125 kPa and 1000 K entering, and leaving at 100 kPa and 400 K. The other line has 0.5 kg/s water entering at 200 kPa and 20 °C, and leaving at 200 kPa. Calculate the exit temperature of the water and the total rate of entropy generation?

Answer 1

120°C

Step-by-step explanation:

Step one:

given data

T_{wi} = 20^{\circ}C

T_{Ai}=1000K

T_{Ae}= 400kPa

P_{Wi}=200kPa

P_{Ai}=125kPa

P_{We}=200kPa

P_{Ae}=100kPa

m_A=2kg/s

m_W=0.5kg/s

We know that the energy equation is

`m_Ah_(Ai)+m_Wh_W=m_Ah_(Ae)+m_Wh_(We)`

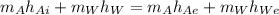
making
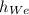`h_(We)` the subject of formula we have

`h_(We)=h_(Wi)+(m_A)/(mW)(h_A-h_(Ae))`

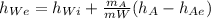
from the saturated water table B.1.1 , corresponding to
`T_(wi)= 20c`

`h_(Wi)=83.94kJ/kg`

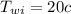
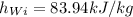
from the ideal gas properties of air table B.7.1 , corresponding to T=1000K

the enthalpy is:

`h_(Ai)=1046.22kJ/kg`

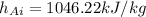
from the ideal gas properties of air table B.7.1 corresponding to T=400K

`h_(Ae)=401.30kJ/kg`

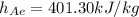
Step two:

substituting into the equation we have

`h_(We)=h_(Wi)+(m_A)/(mW)(h_A-h_(Ae))`

`h_(We)=83.94+(2)/(0.5)(2046.22-401.30)\\\\h_(We)=2663.62kJ/kg`

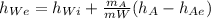
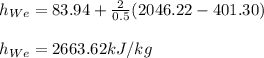
from saturated water table B.1.2 at
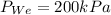`P_(We)=200kPa` we can obtain the specific enthalpy:

`h_g=2706.63kJ/kg`

we can see that
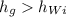`h_g>h_(Wi)`, hence there are two phases

from saturated water table B.1.2 at
`P_(We)=200kPa`

`T_(We)=120 ^(\circ) C`