Question

A particle moves along a line so that its position at any time is t greater than or equal to 0 is given by s(t)=-t^2+t+2 where s is measured in meters and t is measured in seconds. A) what is the initial position of the particle? B) find the velocity of the particle at any time t. C) find the acceleration of the particle at any time t. D) find the speed of the particle at the moment when s(t)=0.

Answer 1

A) The initial position of the particle is 2 meters.

B) The velocity of the particle at any time t is represented by
`v(t) =-2\cdot t +1`.

C) The acceleration of the particle at any time t is represented by
`a(t) = -2`.

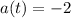D) The velocity of the particle at the moment when
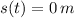`s(t) = 0\,m` is -2 meters per second.

Explanation:

A) From statement we know that
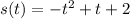`s(t) = -t^(2)+t+2`, where
`t` is the time, measured in seconds, and
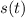`s(t)` is the distance, measured in meters. The initial position of the particle is calculated by evaluating the function presented above at
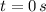`t=0\,s`. That is:

`s(0) = -(0)^(2)+(0)+2`

`s(0) = 2\,m`

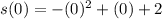
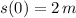
The initial position of the particle is 2 meters.

B) According to the Theory on Kinematics, we see that velocity is the rate of change of position in time. In other words, we need to derive the equation once:

`v(t) =-2\cdot t +1` (1)

Where
`v` is the velocity, measured in meters per second.

The velocity of the particle at any time t is represented by
`v(t) =-2\cdot t +1`.

C) And the acceleration is the rate of change of velocity in time. In other words, we need to derive the equation above:

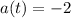`a(t) = -2` (2)

The acceleration of the particle at any time t is represented by
`a(t) = -2`.

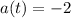D) At first we solve the function position for
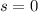`s = 0`, that is:

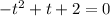`-t^(2)+t+2=0` (3)

`(t-2)\cdot (t+1)=0`

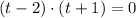
The only reasonable root of the polynomial is
`t = 2\,s`.

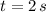And now we evaluated the velocity function at given result:

`v(2) = -2\cdot (2) +2`

`v(2) = -2\,(m)/(s)`

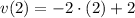
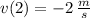
The velocity of the particle at the moment when
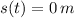`s(t) = 0\,m` is -2 meters per second.