Question

I need help with 2 questions plzzzzz

1. The two lines represented by the equations below are graphed on a coordinate plane. Which statement best describes the two lines? x + 6y = 12 and 3(x -2) =-y-4 *

The lines are parallel.
The lines are the same line.
The lines are perpendicular.
The lines intersect at an angle other than 90°.

2. Triangle Proof: Which type of triangle can be drawn using the points (-2, 3), (=2, -7), and (4, -5)? Use the distance formula to find the length of each side. *

Scalene
Isosceles
Equilateral
No triangle can be drawn

Answer 1

Explanation:

1). x + 6y = 12 ⇔ y =
`-(1)/(6)` x + 2

3(x - 2) = - y - 4 ⇔ y = - 3x + 2

There is not significant relation between slopes such as:

- "the same" for parallel or the same lines;

- "opposite reciprocals" for perpendicular lines;

Thus, there is only answer option left: "The lines intersect at an angle other than 90°."

2). A(- 2, 3), B(- 2, - 7), C(4, - 5)

AC =
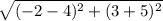`√((-2-4)^2 +(3+5)^2)` = 10

AB = 10

BC =
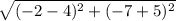`√((-2-4)^2 +(-7+5)^2)` = 2√10

Triangle is Isosceles.