Answer:
D=[0, 8 214.29]
R=[0, 230 000]
Explanation:
In order to find the domain, we must think of the least price you can give to the product you are selling. The price cannot be less than zero, since that would mean that you are giving money to the consumer for taking the product away, so zero is the smallest value p can get.
The greatest value the price can get is the one such that the quantity demanded is zero. So we need to determine that price by setting the equation equal to zero and solving for p.
230,000-28p=0
so we get
-28p=-230,000
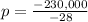
so
p=$8,214.29
so the restricted domain for this function would be:
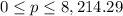
or in interval notation:
D=[0, 8 214.29]
In order to find the range, we just need to determine what's the least and greatest value the function can get. Since this is a linear function, we can find them by just substituting each of the extreme values of the domain in the function, so we get:
q=230,000-28(0)=230,000
q=230,000-28(8214.29)=0
so the range would be:
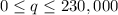
or in interval notation:
R=[0, 230 000]