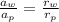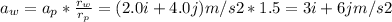Complete Question:
A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns.
They are on the same radial line. At one instant, the acceleration of the purse is (2.00 m/s2 ) i + (4.00 m/s2 ) j .At that instant and in unit-vector notation, what is the acceleration of the wallet
Answer:
aw = 3 i + 6 j m/s2
Step-by-step explanation:
- Since both objects travel in uniform circular motion, the only acceleration that they suffer is the centripetal one, that keeps them rotating.
- It can be showed that the centripetal acceleration is directly proportional to the square of the angular velocity, as follows:
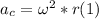
- Since both objects are located on the same radial line, and they travel in uniform circular motion, by definition of angular velocity, both have the same angular velocity ω.
∴ ωp = ωw (2)
⇒
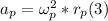
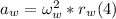
- Dividing (4) by (3), from (2), we have: