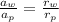Question

A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns. They are on the same radial line. At one instant, the acceleration of the purse is (2.00 m/s2 ) (4.00 m/s2 ) .At that instant and in unit-vector notation, what is the acceleration of the wallet

Answer 1

Complete Question:

A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns.

They are on the same radial line. At one instant, the acceleration of the purse is (2.00 m/s2 ) i + (4.00 m/s2 ) j .At that instant and in unit-vector notation, what is the acceleration of the wallet

Answer:

aw = 3 i + 6 j m/s2

Step-by-step explanation:

• Since both objects travel in uniform circular motion, the only acceleration that they suffer is the centripetal one, that keeps them rotating.
• It can be showed that the centripetal acceleration is directly proportional to the square of the angular velocity, as follows:

`a_(c) = \omega^(2) * r (1)`

• Since both objects are located on the same radial line, and they travel in uniform circular motion, by definition of angular velocity, both have the same angular velocity ω.

∴ ωp = ωw (2)

⇒
`a_(p) = \omega_(p) ^(2) * r_(p) (3)`

`a_(w) = \omega_(w)^(2) * r_(w) (4)`

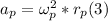
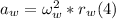
• Dividing (4) by (3), from (2), we have:

`(a_(w) )/(a_(p)) = (r_(w) )/(r_(p))`

• Solving for aw, we get:

`a_(w) = a_(p) *(r_(w) )/(r_(p) ) = (2.0 i + 4.0 j) m/s2 * 1.5 = 3 i +6j m/s2`