Answer:
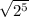
Explanation:
First, deal with the product of the two powers of 2 inside the parentheses.
The two factors are powers of 2, so add the exponents.

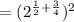
You need a common denominator, 4, to add the fractions.
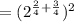
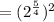
Now you have an exponent raised to an exponent. Multiply the exponents and reduce the fraction.
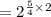
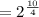
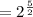
When a fraction is an exponent, the numerator is an exponent and the denominator is the index of the root. A denominator of 2 means a root index of 2 which means square root.
