Question

`\mathrm {Is}`
`\sqrt[]{103}`
`\mathrm {irrational/rational?}`

Answer 1

Yes this is irrational like the guy above me said you cannot write it as a ratio, of integer since rational numbers are:

A rational number is any integer,

fraction,

terminating decimal,

or repeating decimal.

So its Not Rational

Answer 2

Answer: Irrational

We cannot write
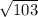`√(103)` as a ratio of integers, so that's why it's irrational.

Note that
`√(103) \approx 10.1488915650922`

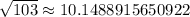
The decimal digits go on forever without any pattern. If the digits repeated themselves, then we would have a rational number.

A quick way to tell if it is rational or not, without using a calculator, is to note that 103 is not a perfect square. The list of perfect squares are:

1,4,9,16,25,36,49,64,81,100,121,...

we see that 100 is the closest perfect square, but 103 is not in that list. Each perfect square is of the form x^2, where x is some positive whole number.