Question

Use the Fundamental Theorem of Calculus to find the "area under curve" of

f
(
x
)
=
6
x
+
19
between
x
=
12
and
x
=
15
.

Answer 1

`\displaystyle A = 300`

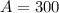
General Formulas and Concepts:

Calculus

Integrals

• Definite Integrals
• Area under the curve
• Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

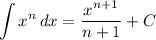
Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

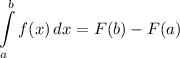
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

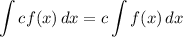
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Area of a Region Formula:
`\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx`

Explanation:

Step 1: Define

Identify

f(x) = 6x + 19

Interval [12, 15]

Step 2: Find Area

1. Substitute in variables [Area of a Region Formula]:
   `\displaystyle A = \int\limits^(15)_(12) {(6x + 19)} \, dx`
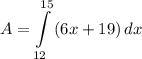
2. [Integral] Rewrite [Integration Property - Addition/Subtraction]:
   `\displaystyle A = \int\limits^(15)_(12) {6x} \, dx + \int\limits^(15)_(12) {19} \, dx`
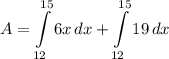
3. [Integrals] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle A = 6\int\limits^(15)_(12) {x} \, dx + 19\int\limits^(15)_(12) {} \, dx`
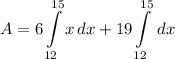
4. [Integrals] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle A = 6((x^2)/(2)) \bigg| \limits^(15)_(12) + 19(x) \bigg| \limits^(15)_(12)`
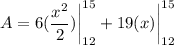
5. Evaluate [Integration Rule - Fundamental Theorem of Calculus 1]:
   `\displaystyle A = 6((81)/(2)) + 19(3)`
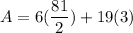
6. Simplify:
   `\displaystyle A = 300`

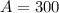
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Book: College Calculus 10e