Question

Tina just opened a new restaurant. She earned $550 on

the first dayand $750 on the third day that she was open
for business. If Samantha's earnings continue to increase
at the same rate, by how much will she earn on the 7th
day? $
SHOW YOUR WORK.
HINT: Find the equation of the line in the Slope Intercept
form and set x = 7.
1) Find the slope.
2) Use the point slope method to get the equation of the line.
Write the equation in Slope Intercept form.
3) Substitute 7 for x to get the answer.​

Answer 1

Samantha will earn $1,150 on the 7th day.

Explanation:

Linear Modeling

It consists of finding the equation of a line that represents the data provided in a specific situation.

Tina's (or Samantha's) earnings are $550, x, $750,... where x is an unknown amount for the second day of her new restaurant.

The earnings continue to increase at the same rate until the 7th day. We must find the earnings for that last day.

The linear model can be found in several ways. We'll use the slope-point form of the line, finding first the slope and then the y-intercept.

The equation of the line in slope-intercept form is:

y=mx+b

Being m the slope and b the y-intercept.

1) Find the slope

Suppose we know the line passes through points A(x1,y1) and B(x2,y2). The slope can be calculated with the equation:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

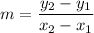
We have the points (1,550) and (3,750), thus:

`\displaystyle m=(750-550)/(3-1)=100`

2) Get the equation of the line

Substituting into the equation of the line, we get:

y=100x+b

Select the point (1,550), substitute into the above equation, and solve for b:

550=100(1)+b

Solving:

b=450

Thus we complete the equation of the linear model:

y=100x+450

3) Substitute 7 for x

y=100(7)+450

y=1,150

Samantha will earn $1,150 on the 7th day.