Question

A lot is 25 m wide and 120 m long. How

many metres must be added to both the
length and the width to increase the area
by 750 square metres?

Answer 1

5 meters must be added to both the length and the width

Explanation:

Area of a Rectangle

A rectangle of width W and length L has an area calculated as:

A = W*L

Initially, the lot has a width of W1=25 m and a length of L1 = 120 m, thus its area is:

`A_1 = 25 * 120 = 3,000~m^2`

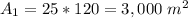
When adding x meters to the width and the length, the new area is:

`A_2=(25+x)(120+x)`

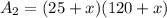
Operating:

`A_2=x^2+145x+3,000`

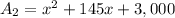
We now calculate the increased area by subtracting A2-A1:

`A=x^2+145x+3,000-3,000`

`A=x^2+145x`

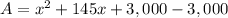
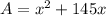
We are given this area is 750 square meters, thus:

`x^2+145x=750`

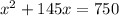
Rearranging:

`x^2+145x-750=0`

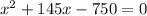
Factoring:

`(x-5)(x+150)=0`

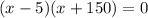
Solving:

x=5, x=-150

Taking the positive solution x=5:

5 meters must be added to both the length and the width