Question

In the complex plane, the rectangular coordinates (x, y) represent a complex number. Which statement explains why polar coordinates (r, θ) represent the same complex number?

Answer 1

Option (2)

Explanation:

From the picture attached,

Let the rectangular coordinates (x, y) is represented by the polar coordinates (r, θ).

By applying Pythagoras theorem in ΔPAO,

PO² = AO² + AP²

r² = x² + y²

r =
`√(x^2+y^2)`

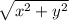
By applying tangent rule in ΔAPO,

tanθ =
`(AP)/(OA)`

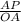
tanθ =
`(y)/(x)`

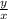
θ =
`\text{tan}^(-1)((y)/(x))`

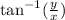
Therefore, Option 2 will be the correct option.