Answer:
-8
Explanation:
Convert the equation from standard form into slope-intercept form by....
- Moving the variable to the right-hand side and change its sign: 6y = 10 - 4x
- Divide both sides of the equation by 6 : y=
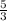 -
-
 x
x
- Use the commutavie property to reoder the terms : y= -
 x +
x +
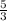
(Parallel lines have the same slope.. so the slope = -
 )
)
Create and equation using the slope and the point (k,7)
- Make the equation : 7 = -
 (k) +
(k) +
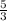
- Multiply both sides of the equation by 3 : 21 = -2k + 5
- Move the varable to the left-hand side and change its sign: 2k + 21 = 5
- Move the constant to the right-hand side and change its sign: 2k + 5 - 21
- Calculate the difference: 2k = -16
- Divide both sides of the equation by 2 : k= -8
Solution : k = -8