Answer:
Explanation:
Given function is,

Factors of the numerator = x² - 3x + 2
= x² - 2x - x + 2
= x(x - 2) - 1(x - 2)
= (x - 2)(x - 1)
Therefore, given function will be,
f(x) =
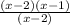
For (x - 2) = 0
For x = 2, denominator will become zero.
Thus for input value x = 2, function will not be defined.
If x ≠ 2, f(x) = x - 1
It's a linear function represented by f(x) = x - 1
Having slope = 1 and y-intercept = -1
And (2, 1) is a hole as shown in the graph.