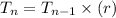Answer:
Explanation:
Question (1)
From the table showing arithmetic sequence,
First term of the sequence = 18
5th term of the sequence = -10
Explicit formula of an arithmetic sequence,
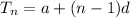
For 5th term,
-10 = 18 + (5 -1)d
-10 = 18 + 4d
4d = -28
d = -7
Therefore, explicit formula for the table will be,
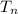 = 18 + (n - 1)(-7)
= 18 + (n - 1)(-7)
= 18 - 7n + 7
= 25 - 7n
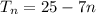
Recursive formula →
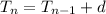
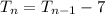
Question (2),
From the table attached,
First term of the geometric sequence = 6
5th term = 96
Recursive formula of a geometric sequence =
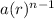
Here a = first term
r = common ratio
For 5th term from the table,
96 =
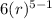
r⁴ = 16
r =
![\sqrt[4]{16}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/d0406k6nhwecnfw1kagv1xdg2w2df87ate.png)
r = 2
Therefore, explicit formula will be,
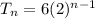
Recursive formula will be,