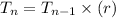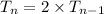Question

Does someone know how to do this??

Answer 1

Explanation:

Question (1)

From the table showing arithmetic sequence,

First term of the sequence = 18

5th term of the sequence = -10

Explicit formula of an arithmetic sequence,

`T_(n)=a+(n-1)d`

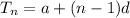
For 5th term,

-10 = 18 + (5 -1)d

-10 = 18 + 4d

4d = -28

d = -7

Therefore, explicit formula for the table will be,

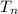`T_n` = 18 + (n - 1)(-7)

= 18 - 7n + 7

= 25 - 7n

`T_n=25-7n`

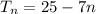
Recursive formula →
`T_n=T_(n-1)+d`

`T_n=T_(n-1)-7`

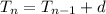
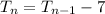
Question (2),

From the table attached,

First term of the geometric sequence = 6

5th term = 96

Recursive formula of a geometric sequence =
`a(r)^(n-1)`

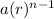
Here a = first term

r = common ratio

For 5th term from the table,

96 =
`6(r)^(5-1)`

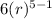
r⁴ = 16

r =
`\sqrt[4]{16}`

r = 2

Therefore, explicit formula will be,

`T_n=6(2)^(n-1)`

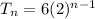
Recursive formula will be,

`T_n=T_(n-1)* (r)`

`T_n=2* T_(n-1)`