Answer:
x=60,150,240,330
Explanation:
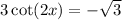
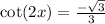
Take the arc cot of both sides
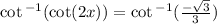
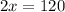
Remember cotangent has a period of 180 degrees
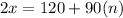
where n is 0, 1,2,3,4,5.....
Isolate x.
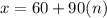
where n is 0, 1,2,3,4,5,6.
Keep plugging in integers as long they are in the interval [0,360].
We get
60,150,240,330.