Question

Solve 3cot (2x) =- Route3 for
x, 0 = x < 360

Answer 1

x=60,150,240,330

Explanation:

`3 \cot(2x) = - √(3)`

`\cot(2x) = ( - √(3) )/(3)`

Take the arc cot of both sides

`\cot {}^( - 1) ( \cot(2x) ) = \cot {}^( - 1) ( ( - √(3) )/(3) )`

`2x = 120`

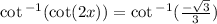
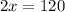
Remember cotangent has a period of 180 degrees

`2x = 120 + 90(n)`

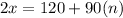
where n is 0, 1,2,3,4,5.....

Isolate x.

`x = 60 + 90(n)`

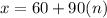
where n is 0, 1,2,3,4,5,6.

Keep plugging in integers as long they are in the interval [0,360].

We get

60,150,240,330.