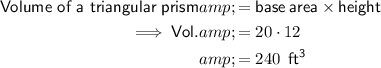Answer:
Lateral Surface Area: The total surface area of a three-dimensional object, excluding the bases.
Question 5
Figure: Rectangular prism
Given:
- length (
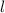 ) = 10 m
) = 10 m - width (
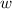 ) = 4 m
) = 4 m - height (
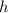 ) = 6 m
) = 6 m
Lateral Surface Area
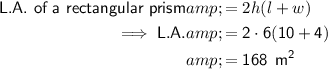
Total Surface Area
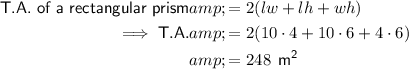
Volume

Question 6
Figure: Triangular Prism
The bases of a triangular prism are the triangles.
First, find the hypotenuse of the right triangular base using Pythagoras' Theorem
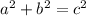 where a and b are the legs and c is the hypotenuse.
where a and b are the legs and c is the hypotenuse.

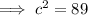
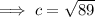
Lateral Surface Area
The L.A. is made up of 3 rectangles, each with a length of 12 ft and a width of one side of the triangular base.
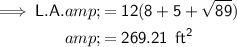
Total Surface Area
The T.A. is made up of the L.A. plus the areas of the triangular bases.
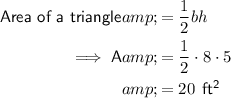
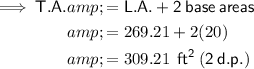
Volume