Question

100 POIntsSarah has been running a dog-walking business since 2010. She walks dogs twice a day, takes them to the park, and returns them to their homes. Each year, she has increased her fee by the same amount. The table shows what Sarah charged each customer for two given years of her business:

Year Annual Dog-walking Fee
2010 $350
2014 $750
A. What is the rate of change and initial value for Sarah's business? How do you know?
B. Write an equation in slope-intercept form to represent the fees that Sarah charges each year. (10 points)

Answer 1

----------------------------------------------------------------------------------------------------------

Problem (a):
`\textsf{Rate of change = \$100 per year, Initial value = \$350}`

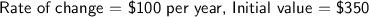
Problem (b):
`\textsf{y = 100x + 350}`

----------------------------------------------------------------------------------------------------------

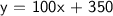
The first step that we must take before attempting to solve the problem is to understand what the problem is asking us to do and what is given to us to help do so. So in the first part we are asked what the rate of change and initial value for Sarah's business. Using that information we would be able to complete the second part which asks us to write an equation in slope-intercept form. In this problem we are given two points which resemble how much Sarah charged each customer for the given years.

Now that we know what we must accomplish, we can move onto actually solving the problem. So first we must determine what the rate of change is and this is basically like finding the slope. This can be done by subtraction the y-values in the numerator and the x-values in the denominator.

Determine the rate of change

• 
  `m = (y_2 - y_1)/(x_2 - x_1)`

• 
  `m = (750 - 350)/(2014 - 2010)`

• 
  `m = (400)/(4)`

• 
  `m = 100`

Now we can see that the rate of change would be an increase of $100 per year after calculating the slope. The next part was to determine the initial value for Sarah's business and this can be easily done because we know that she has had this business since 2010 and we are given that the price in 2010 was $350.

----------------------------------------------------------------------------------------------------------

We now have completed part (a) and we can move onto the next part which is to create an equation in slope-intercept form to represent the fees that Sarah charges each year.

So we know that the slope is an increase of $100 per year which means that we will have a positive slope. We also know the initial price that Sarah charged in her first year which will represent the y-intercept or the first point on the graph.

• m ⇒ This represents the slope of the line that is being written.

• b ⇒ This represents the y-intercept of the line that is being written.

Plug in the values

• 
  `y = mx + b`

• 
  `y = 100x + 350`

After plugging in the values we have a finished expression in slope-intercept form which represents the scenario that is going on with Sarah's business. We see that that initial price was 350 and we increase that by 100 each year. Therefore, the final equation in slope-intercept form is y = 100x + 350.

----------------------------------------------------------------------------------------------------------